Omvendt funktion
En funktion er som bekendt en sammenhæng, der til en størrelse, argumentet, knytter en anden størrelse, værdien. For hvert argument er der netop én værdi. Vi benytter ofte bogstavet \(x\) for argumentet, og kalder det den uafhængige variabel, mens vi benytter bogstavet \(y\) for værdien, og kalder det den afhængige variabel. Mængden af alle tilladte argumenter kaldes definitionsmængden, mens mængden af tilhørende værdier betegnes værdimængden.
Som et eksempel kan vi betragte sammenhængen mellem arbejdstid og lønudbetaling for en timelønnet person. Her afhænger lønnen naturligvis af antallet af arbejdstimer, hvorfor den uafhængige variabel er arbejdstiden og den afhængige variabel er lønnen. Vi kan skrive
| \(x\) | Antal arbejdstimer |
| \(y\) | Lønudbetaling i kroner |
Hvis timelønnen er 100 kroner, så er sammenhængen (funktionen) \[ y=100x. \] Ofte vælger vi at give vores funktion et navn, for eksempel \(f\), og så skriver vi \(f(x)\) i stedet for \(y\). I dette tilfælde får vi så forskriften \[ f(x)=100x. \]
Vi har tit brug for at regne baglæns. Hvis personen i løneksemplet får udbetalt en løncheck på \(3\hspace{0.1666666666666667em}000\) kroner, så ønsker vi måske at finde ud af, hvor mange arbejdstimer, der er gået forud, og hvis personen har planer om at købe en bil til \(90\hspace{0.1666666666666667em}000\) kroner, så vil vi gerne vide, hvor mange arbejdstimer, det vil kræve. Her ville det være rart, hvis vi havde en funktion, der kunne bringe os tilbage fra \(y\) til \(x\). Det er ikke svært at finde sådan en funktion. Da det modsatte af at gange med 100 er at dividere med 100, er \[ x=\frac{y}{100}. \] Hvis vi kalder den funktion, der sender \(y\) tilbage i \(x\) for \(g\), så kan vi skrive \(g(y)\) i stedet for \(x\), hvilket giver forskriften \[ g(y)=\frac{y}{100}. \] Den nye funktion går i den modsatte retning af \(f\), og den bringer os tilbage til udgangspunktet i den forstand at \(g(f(x))=x\). Hvis vi i stedet starter med \(g\) og derefter anvender \(f\) kommer vi også tilbage til udgangspunktet, dvs. \(f(g(y))=y\). Der gælder med andre ord, at \(f(x)=y\), hvis og kun hvis \(g(y)=x\).
Vi giver nu en mere formel definition af omvendt funktion. En funktion \(f:X\to Y\) siges at have en omvendt funktion (eller at være invertibel), hvis der findes en funktion \(g:Y\to X\), så \(g(f(x))=x\) for alle \(x\in X\) og \(f(g(y))=y\) for alle \(y\in Y\). Ved hjælp af funktionssammensætning kan dette omformuleres til, at \(g\circ f=\id_X\) og \(f\circ g=\id_Y\) hvor \(\id_X\) og \(\id_Y\) er identitetsfunktionerne på henholdsvis \(X\) og \(Y\). Vi kalder \(g\) den omvendte funktion til \(f\), og vi skriver også \(f^{-1}\) i stedet for \(g\).
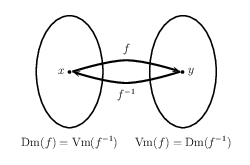
I definitionen ovenfor indgår funktionerne \(f\) og \(g\) symmetrisk. Det betyder, at \(g\) også har en omvendt funktion, nemlig \(f\). Sagt med andre ord: Hvis \(f\) har en omvendt funktion \(f^{-1}\), så har \(f^{-1}\) også en omvendt funktion, og \(\left(f^{-1}\right)^{-1}=f\). De to funktioner \(f\) og \(f^{-1}\) er altså hinandens omvendte funktioner.
Endnu et eksempel er funktionen \(f:\{-2,-1,0,1,2\}\to\{1,2,3,4,5\}\) givet ved \(f(x)=x+3\). Det modsatte af at lægge tre til er at trække tre fra, hvorfor \(f^{-1}:\{1,2,3,4,5\}\to\{-2,-1,0,1,2\}\) har forskriften \(f^{-1}(y)=y-3\).
Som illustreret nedenfor bytter den omvendte funktion om på definitions- og værdimængde. Desuden vender den omvendte funktion pilene.

Hvilke funktioner har en omvendt funktion?
Det er ikke alle funktioner, der har en omvendt funktion. Man kan vise, at en funktion \(f:X\to Y\) har en omvendt funktion, hvis og kun hvis \(f\) er bijektiv. Funktionen \(f\) har altså en omvendt funktion \(f^{-1}\), hvis og kun hvis der for ethvert \(y_0\in Y\) er netop ét \(x_0\in X\), så \(f(x_0)=y_0\). I bekræftende fald er \(f^{-1}(y_0)=x_0\).
Det er svært at vise, at enhver bijektiv funktion har en omvendt funktion, så det gør vi ikke her. Til gengæld gør vi nedenfor rede for, at kun bijektive funktioner kan have en omvendt funktion.
Antag at vi har to funktioner \(f:X\to Y\) og \(g:Y\to X\), der opfylder, at \(g\circ f=\id_X\). Så må \(f\) være injektiv. Antag nemlig, at \(x_1,x_2\in X\) og \(f(x_1)=f(x_2)\). Så er \(g(f(x_1))=g(f(x_2))\). Men \(g(f(x_1))=x_1\) og \(g(f(x_2))=x_2\) ifølge antagelsen, og derfor er \(x_1=x_2\). Det viser, at \(f\) er injektiv.
Antag at vi har to funktioner \(f:X\to Y\) og \(g:Y\to X\), der opfylder, at \(f\circ g=\id_Y\). Så må \(f\) være surjektiv. Til givet \(y_0\in Y\) kan vi nemlig sætte \(x_0=g(y_0)\). Så er \(f(x_0)=f(g(y_0))=y_0\). Det viser, at \(f\) er surjektiv.
En funktion \(f:X\to Y\) har en omvendt funktion, hvis der findes en funktion \(g:Y\to X\), så \(g\circ f=\id_X\) og \(f\circ g=\id_Y\). Vi har lige vist, at hvis \(g\circ f=\id_X\), så er \(f\) injektiv, og hvis \(f\circ g=\id_Y\), så er \(f\) surjektiv. Altså er enhver invertibel funktion både injektiv og surjektiv. Det vil sige, at enhver invertibel funktion er bijektiv.
Bemærk at spøgrsmålet om en funktion har en omvendt funktion ikke alene afhænger af funktionens forskrift. Det afhænger også af funktionens definitions- og sekundærmængde. Betragt for eksempel funktionen \(g:[0;\infty[\hspace{0.1666666666666667em}\to\Bbb{R}\) givet ved \(g(x)=\sqrt{x}\) og funktionen \(h:[0;\infty[\hspace{0.1666666666666667em}\to[0;\infty[\hspace{0.1666666666666667em}\) givet ved \(h(x)=\sqrt{x}\). Den eneste forskel på de to funktioner er deres sekundærmængde. Da de to funktioner har samme definitionsmængde og forskrift, er der i en vis forstand tale om den samme funktion, men \(h\) er surjektiv, og det er \(g\) ikke. Derfor har \(h\) en omvendt funktion, og det har \(g\) ikke.
En funktions definitionsmængde kan også have betydning for, om funktionen har en omvendt funktion eller ej. For at kunne give et eksempel benytter vi, at der for et positivt tal gælder, at hvis man først tager kvadratet på tallet og derefter kvadratroden, så kommer man tilbage til udgangspunktet, men dette gælder ikke for negative tal. For eksempel er \(\sqrt{2^2}=\sqrt{4}=2\) og \(\sqrt{(-2)^2}=\sqrt{4}=2\ne -2\). For positive tal gælder der \(\sqrt{x^2}=x\) og for negative tal er \(\sqrt{x^2}=-x\). Ved at benytte den numeriske værdi kan dette samles i en formel: \[ \sqrt{x^2}=|x|. \] Nedenfor viser vi, at kvadratfunktionen har en omvendt funktion, når vi definerer den på de ikke-negative reelle tal (eller på de ikke-positive reelle tal), men ikke når vi definerer den på alle de reelle tal.
Lad \(f:\Bbb{R}\to [0;\infty[\hspace{0.1666666666666667em}\) være givet ved \(f(x)=x^2\). Det er klart, at \(f\) ikke er injektiv, da for eksempel \(f(-2)=f(2)\). Derfor har \(f\) ikke en omvendt funktion. Hvis vi definerer \(g:[0;\infty[\hspace{0.1666666666666667em}\to\Bbb{R}\) ved \(g(x)=\sqrt{x}\), så er det klart, at \(f\circ g=\id_{[0;\infty[}\hspace{0.1666666666666667em}\), men \(g\circ f\) er ikke lig med identitetsfunktionen på \(\Bbb{R}\). Faktisk gælder der \[ (g\circ f)(x)=g(f(x))=g(x^2)=\sqrt{x^2}=|x|, \] dvs. \(g\circ f\) er funktionen på \(\Bbb{R}\), der tager den numeriske værdi af et tal.
Selvom \(f\) ikke er injektiv, så findes der restriktioner af \(f\), der er injektive. Vi kan for eksempel tage restriktionen til \(]-\infty;0]\) eller til \([0;\infty[\hspace{0.1666666666666667em}\). Sæt \(f_1=f|_{]-\infty;0]}\) og \(f_2=f|_{[0;\infty[}\hspace{0.1666666666666667em}\). Det er klart, at \(f_1\) og \(f_2\) begge er bijektive funktioner. Dermed har de omvendte funktioner. Der gælder \(f_1^{-1}(x)=-\sqrt{x}\) og \(f_2^{-1}(x)=\sqrt{x}\). På figuren nedenfor ses graferne for \(f_1\) og \(f_2\) og deres omvendte funktioner. Grafen for \(f_1\) er lyseblå og grafen for \(f_1^{-1}\) er lysegrøn. Grafen for \(f_2\) er mørkeblå og grafen for \(f_2^{-1}\) er mørkegrøn.
Forskrift for den omvendte funktion
Antag at funktionen \(f:X\to Y\) har en omvendt funktion \(f^{-1}:Y\to X\). Så gælder der \(f(x)=y\), hvis og kun hvis \(f^{-1}(x)=y\). Det betyder, at hvis \(f\) har en forskrift \(f(x)=\text{udtryk i \(x\)}\), så kan vi finde en forskrift for \(f^{-1}\) ved at løse ligningen \(y=\text{udtryk i \(x\)}\) med hensyn til \(x\), dvs. omskrive ligningen til \(x=\text{udtryk i \(y\)}\). Nu får vi en forskrift for \(f^{-1}\) ved at erstatte \(x\) med \(f^{-1}(y)\). For at finde en forskrift for den omvendte funktion til \(f\) skal vi altså gennemløbe følgende trin:
- Erstat “\(f(x)=\text{udtryk i \(x\)}\)” med “\(y=\text{udtryk i \(x\)}\)”
- Isolér \(x\)
- Erstat “\(x=\text{udtryk i \(y\)}\)” med “\(f^{-1}(y)=\text{udtryk i \(y\)}\)”
- Erstat eventuelt \(y\) med \(x\) på begge sider af lighedstegnet
Som et eksempel kan vi endnu engang betragte funktionen \(f(x)=x+3\). Første trin er at erstatte \(f(x)\) med \(y\), hvilket giver \(y=x+3\). Andet trin er at isolere \(x\). Det gør vi ved at trække \(3\) fra på begge sider af lighedstegnet. Det giver \(y-3=x\), der også kan skrives \(x=y-3\). Tredje trin er at erstatte \(x\) med \(f^{-1}(y)\). Dette giver os igen forskriften \(f^{-1}(y)=y-3\). Fjerde trin er at erstatte \(y\) med \(x\). Vi får nu \(f^{-1}(x)=x-3\).
Lad os se på et mere kompliceret eksempel, nemlig funktionen \(g(x)=2x+2\). Denne funktion er bijektiv, og har dermed en omvendt funktion \(g^{-1}\). For at finde en forskrift for \(g^{-1}\) starter vi med at erstatte \(g(x)\) med \(y\) i forskriften for \(g\), hvilket giver os ligningen \[ y=2x+2. \] For at løse denne ligning med hensyn til \(x\), trækker vi først \(2\) fra på begge sider af lighedstegnet, hvilket giver \[ y-2=2x, \] og derefter dividerer vi med \(2\) på begge sider af lighedstegnet, og får \[ \frac{y-2}{2}=x. \] Dette kan også skrives \(x=\frac{1}{2}y-1\). Når vi erstatter \(x\) med \(g^{-1}(y)\), får vi forskriften \[ g^{-1}(y)=\frac{1}{2}y-1. \] Vi kan også skrive forskriften på mere velkendt form med \(x\) i stedet for \(y\): \[ g^{-1}(x)=\frac{1}{2}x-1. \] Nedenfor ses graferne for \(g\) (blå) og \(g^{-1}\) (grøn).
Grafen for den omvendte funktion
Grafen for \(f\) består af de punkter \((x,y)\), der opfylder \(y=f(x)\). Hvordan ser grafen for den omvendte funktion ud? Svaret er, at det afhænger af, om vi anvender \(x\) eller \(y\) som den uafhængige variabel for \(f^{-1}\). Hvis vi anvender \(y\) som uafhængig variabel, så består grafen for \(f^{-1}\) af de punkter \((x,y)\), der opfylder \(x=f^{-1}(y)\). Det betyder, at \(f^{-1}\) har samme graf som \(f\), idet der gælder \(x=f^{-1}(y)\), hvis og kun hvis \(y=f(x)\).
Hvis vi derimod benytter \(x\) som uafhængig variabel, hvilket man normalt gør, når man skal tegne grafen, så er \(y=f^{-1}(x)\). Det betyder, at vi har byttet om på \(x\) og \(y\), hvilket svarer til at spejle i linjen \(y=x\). Denne linje er indtegnet stiplet i figuren nedenfor. Desuden ses grafen for \(f(x)=\frac{1}{2}x\) (blå) og grafen for \(f^{-1}(x)=2x\) (grøn). Når vi tager et tilfældigt punkt på grafen for \(f\) som f.eks. \((4,2)\) og spejler det i linjen \(y=x\), så bliver det ført over i punktet \((2,4)\) der ligger på grafen for \(f^{-1}\). Vi kan derfor finde grafen for den omvendte funktion ved at tage grafen for \(f\) og spejle den i linjen \(y=x\).
Hvis funktionen \(f\) har en omvendt funktion \(f^{-1}\), og hvis vi har et sildeben for \(f\), så kan vi finde et sildeben for \(f^{-1}\) ved at bytte om på de to rækker og derefter bytte om på \(x\) og \(y\). For eksempel har funktionen \(f(x)=\frac{1}{2}x\) følgende sildeben:
| \(x\) | \(-5\) | \(-4\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
| \(y=f(x)\) | \(-2.5\) | \(-2\) | \(-1.5\) | \(-1\) | \(-0.5\) | \(0\) | \(0.5\) | \(1\) | \(1.5\) | \(2\) | \(2.5\) |
Ved at bytte om på de to rækker får vi et sildeben for den omvendte funktion:
| \(x\) | \(-2.5\) | \(-2\) | \(-1.5\) | \(-1\) | \(-0.5\) | \(0\) | \(0.5\) | \(1\) | \(1.5\) | \(2\) | \(2.5\) |
| \(y=f^{-1}(x)\) | \(-5\) | \(-4\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
